The Problem

You are given an integer array 'nums' with no duplicates. A maximum binary tree can be built recursively from 'nums' using the following algorithm:

1. Create a root node whose value is the maximum value in 'nums'.
2. Recursively build the left subtree on the subarray prefix to the left of the maximum value.
3. Recursively build the right subtree on the subarray suffix to the right of the maximum value.

Return the maximum binary tree built from 'nums'.

Example 1:

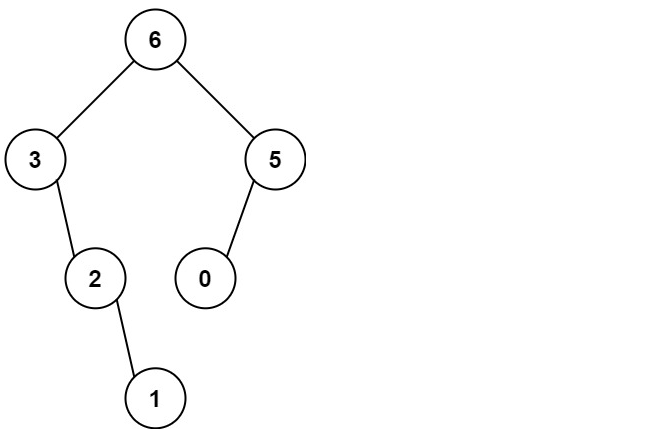
Input: nums = [3,2,1,6,0,5]

Output: [6,3,5,null,2,0,null,null,1]

Explanation: The recursive calls are as follow:

- The largest value in [3,2,1,6,0,5] is 6. Left prefix is [3,2,1] and right suffix is [0,5].

- The largest value in [3,2,1] is 3. Left prefix is [] and right suffix is [2,1].

- Empty array, so no child.

- The largest value in [2,1] is 2. Left prefix is [ ] and right suffix is [1].

- Empty array, so no child. - Only one element, so child is a node with value 1.

- The largest value in [0,5] is 5. Left prefix is [0] and right suffix is [ ].

- Only one element, so child is a node with value 0.

- Empty array, so no child.

Example 2:

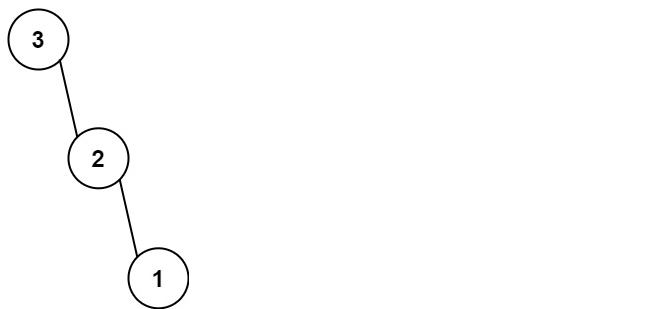
Input: nums = [3,2,1]

Output: [3,null,2,null,1]

Problem Solving Approach

We will identify what we are given, what we need to return and break down a method to get from point A to B in small steps. Then we will combine those steps to form the full solution.

Given

We are given an array of integers. This array of integers has no duplicates. We are also given the class for creating 'TreeNodes'. This is a standard binary tree class.

class TreeNode:
  def __init__(self, val=0, left=None, right=None):
    self.val = val
    self.left = left
    self.right = right

Return

We return the head of a binary tree with name 'node'. This binary tree contains one node for each number in 'nums'. This 'node' that we return contains the value of the greatest number in 'nums'. We then break 'nums' up into two smaller arrays: one array called 'prefix' containing the values on the left of the 'node' and one called 'suffix' containing the values to the right of the 'node'. We then repeat this process with 'prefix' and 'suffix'. We need to find the max value of prefix and make it the left child of the root. Then break prefix into smaller arrays and so on until the they can not be broken down any longer. The process is the same with 'suffix', just on the right side instead of the left.

The Approach

This repeating pattern tends to lend itself to recursion. In this problem, we are specifically told that this can be built recursively. But before we get into the recursion, it is best to establish what the function itself does. It needs to do a few things:

1. Find the max value in 'nums' (remember that there are no duplicates so there will always be only one max value)

2. Create the TreeNode with that value

3. Create the prefix and suffix arrays

1. Finding the Max Value

There is a simple Python function for this:

new_val=max(nums)

2. Creating the Node

After implementing the TreeNode constructor which was given:

node=TreeNode(new_val)

# The above code is what will be in the function
# Below is the constructor needed somewhere in the code that allows TreeNodes to be created
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right

3. Creating the Prefix and Suffix Arrays

There are many ways to do this. One simple way is to use the colon operator. This essentially allows you to slice part of an array at a given index, leaving you with a section of the original. So we first need to identify the index to slice from. This will be the index of the greatest value, which has been identified and stored as 'new_val' in step one.

split_index=nums.index(new_val) # grabbing the index of max value
prefix = nums[:split_index] # slicing out everything before the max value
suffix = nums[split_index+1:] # slicing out everything after the max value

# example input
# nums = [3, 2, 1, 6, 0, 5]

# example outputs
# new_val = 6
# split_index = 4
# prefix = [3, 2, 1]
# suffix = [0, 5]

Recursion

Now that we have the prefix and suffix arrays, what do we do with them? This is where the recursion gets implemented. The whole function is called again using the prefix. The new TreeNode that this creates belongs as the left child of the original TreeNode. This gives us the location to recursively call the function: 'node.left'. This process will work the same way with suffix at 'node.right'.

# check to see if prefix or suffix are empty arrays before calling the function with an empty array
if len(prefix): 
  node.left=constructMaximumBinaryTree(prefix)
if len(suffix):
  node.right=constructMaximumBinaryTree(suffix)

Since the function calls itself , there will be an infinite loop if there is no base case. In each call of this function, the array gets smaller until eventually there are no numbers left in it. This will be the case when the numbers have all been used to create nodes. This is base case. This can be checked right at the beginning of the function so the function returns before it can call itself again.

# the base case 
# goes right at the start of the function
if nums is None:
    return None

Solution

Properly combining all of these parts creates code that solves this problem given any input array that follows the rules of what can be given.

def max_binary_tree(nums):
    if nums is None:
        return None

    new_val=max(nums)
    node=TreeNode(new_val)
    split_index=nums.index(new_val)
    prefix = nums[:split_index]
    suffix = nums[split_index+1:]
    if len(prefix):
        node.left=max_binary_tree(prefix)
    if len(suffix):
        node.right=self.max_binary_tree(suffix)
    return node
        
class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

Time Complexity

The recursive function is called N times where N is the length of 'nums'.

In recursion, there is also a call stack of functions waiting to execute. The length of the call stack can vary depending the problem. In the worst case, this also takes N time. The average case is log(N) time. However, when evaluating time complexity, the worst case must be considered.

Therefore, the time complexity is O(N^2).

Space Complexity

This process takes space as well as time. While it adds O(N) time in the worst case, it also adds O(N) space. This makes the space complexity O(N).