The Problem

Given n non-negative integers a1, a2, ..., an , where each represents a point at coordinate (i, ai). n vertical lines are drawn such that the two endpoints of the line i is at (i, ai) and (i, 0). Find two lines, which, together with the x-axis forms a container, such that the container contains the most water.

Notice that you may not slant the container.

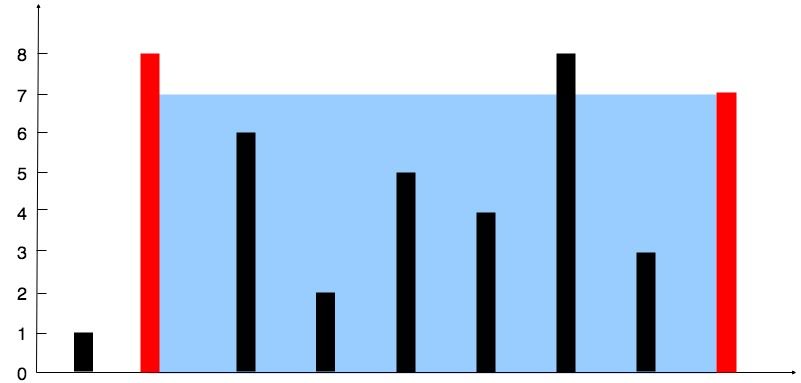
Input: height = [1,8,6,2,5,4,8,3,7]

Output: 49

Explanation: The above vertical lines are represented by array [1,8,6,2,5,4,8,3,7]. In this case, the max area of water (blue section) the container can contain is 49.

Solution

Given

You are given an array of N non-negative integers. Imagine the array as a set of walls in which each integer represents the height of a wall. Its index represents its location relative to the other walls. Any two walls can be used to contain a specific amount of water. The amount of water two walls can hold is equal to the area.

• Area = height of the shorter of the two walls * distance between the walls

When finding the area at two walls, you ignore all the walls in between them.

Return

You return a single number. This number represents an area. Specifically, it represents the maximum possible area that can be created using two walls in the input array.

Approach One (Brute Force)

The first approach idea that may come to mind is brute fore approach wherein you check the area that will be created with every single possible combination of walls.

This approach will:

• Use a for loop with a nested for loop to check every possible area.
• Store a max area.
• Within each iteration, it will calculate the area, compare it to the max area, and replace the max area if it is greater.
• Return the max area.

Things to consider:

• This approach will give you the correct answer.
• The time complexity is O(N^2) because of the nested for loop.

Approach Two (Pointers)

Although approach one works, there is a way to solve the problem in O(N) time. Approach two will utilize a single while loop as opposed to a for loop with an additional for loop nested inside. Consider that every single possible combination of walls does not need to be checked. An algorithm can be implemented that uses the information at each iteration to decide how to proceed through the single for loop in a way that still guarantees the max area will be found at some point. This is done using pointers. One pointer will be initialized to the beginning of the array and other will be initialized to the end.

Similarities to approach one:

• Everything done within an iteration will be nearly the same.
• An area calculation will be made with the two current walls.
• A comparison to the max area will be made with the current area.
• At the end of the loop, the max area will be returned.

Differences to approach one:

• The differences show up when looking at how to proceed through the loop.
• The pointers method has two pointers and just one pointer will move at every iteration.
• A pointer is just a variable used to reference an index in the array.
• The left pointer only moves right and the right pointer only moves left, guaranteeing one pointer will move towards the other at each iteration.
• The loop will stop when the pointers point to the same index.
• Whichever pointer references the index with a lower value is the one that will move inwards.
• If the values are the same, it does not matter which pointer moves.

Things to consider:

• Note that this does not simply hone in on the max area and return it as soon as it is found. Since the array is unsorted, there would be no way to know exactly when the max value is reached until all the values are checked.
• The magic of this method is simply that you will still be guaranteed to find the max area at some point in the loop. It may even be found in the first iteration, but there is no way to know without checking the rest of the array.
• In fact, it actually becomes decreasingly likely you will find the max area as you move your pointers inwards. This is because the width (a factor in calculating the area) will decrease by one every iteration. To make up for the known decrease in width at every iteration, the idea is to replace the index that corresponds to the lower height in hopes of making up for the decreasing width with a new larger height. It is entirely possible to be actually decrease your height at the next iteration, but as previously stated, there would be now way to know until you check it. This method simply uses its current height information to take
• the best guess of how to increase max area if possible.

Below is raw code, the same code with comments, and again with an example.

Raw Code

// raw code
function water(array) {
  let currentArea = 0
  let maxArea = 0
  let left = 0
  let right = array.length - 1

  while (left < right) {
    currentArea = areaCalculator(left , right, array)
    maxArea = Math.max(maxArea, currentArea)
    if (array[left] > array[right]) {
      right--
    } else {
      left++
    }
  }
  return maxArea
}

function areaCalculator(i, j, array) {
  let height = Math.min(array[i], array[j]) 
  let width = j - i 
  let area = width * height
  return area
}

Code With Comments

// with notes
function water1(array) {
  // initialize variables
  let currentArea = 0 // will be recalculated at every iteration
  let maxArea = 0 // will be replaced by current area whenever current area is greater, will be returned at the end
  let left = 0 // used to reference an index in the array, initialized to the beginning index
  let right = array.length - 1 // used to reference an index in the array, initialized to the end index

  // while loop to find maxArea
  while (left < right) { // the loop continues until every index is checked once
    currentArea = areaCalculator(left , right, array) // use the information at the two current indices to find the current area
    maxArea = Math.max(maxArea, currentArea) // overwrite the maxArea value if appropriate
    if (array[left] > array[right]) { // determine which pointer to move toward the center
      right--
    } else {
      left++
    }
  }
  return maxArea
}

function areaCalculator1(i, j, array) {
  let height = Math.min(array[i], array[j]) // find the lower of the two heights based on the values at their indices
  let width = j - i // calculate width based on the two indices
  let area = width * height
  return area
}

Code with an Example

// with example
function water2(array) {
  let currentArea = 0
  let maxArea = 0
  let left = 0
  let right = array.length - 1 // 3

  // each '|' separates the values for each iteration
  while (left < right) { // 0 < 3 | 1 < 3 | 2 < 3 | 3 < 3 is false, end loop
    currentArea = areaCalculator(left , right, array) // 9 | 10 | 7
    maxArea = Math.max(maxArea, currentArea) // 9 | 10 | 10
    if (array[left] > array[right]) { // false | false | false
      right--
    } else {
      left++
    }
    // left = 1, right = 3 | left = 2, right = 3 | left = 3, right = 3
  }
  return maxArea // 10
}

function areaCalculator2(i, j, array) {
  let height = Math.min(array[i], array[j]) // 3 | 5 | 7
  let width = j - i // 3 | 2 | 1
  let area = width * height // 9 | 10 | 7
  return area // 9 | 10 | 7
}